 01
01 02
02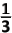 n (n + 1)(n + 2)
n (n + 1)(n + 2)
 65
65 C4
C4 H7
H7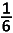 n(n+1)(2n+13)
n(n+1)(2n+13)
 I6
I6 17
17 n (3n − 1)
n (3n − 1)
 M8
M8 N3
N3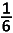 n(2n2+ 9n+1)
n(2n2+ 9n+1)
 O3
O3 L2
L2 36
36 38
38 K4
K4 03
03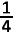 n(n+1)(n+2)(n+3)
n(n+1)(n+2)(n+3)
 39
39 40
40 O2
O2 41
41 42
42 43
43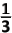 n.(4n² + 6n − 1)
n.(4n² + 6n − 1)
 47
47 S1
S1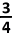 [ (2n − 1).3n + 1]
[ (2n − 1).3n + 1]
 59
59 36
36 37
37 I3
I3 n2(n+1)2(2n2+2n−1)
n2(n+1)2(2n2+2n−1)
 I5
I5 06
06 10
10 C5
C5 J5
J5 O5
O5 B5
B5 67
67 91
91 H8
H8 70
70 (−1)n−1.n.(n+1)
(−1)n−1.n.(n+1)
 72
72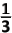 n.(4n2 − 1)
n.(4n2 − 1)
 64
64 96
96 A0
A0 (n+1)(3n+2)
(n+1)(3n+2)
 A6
A6 A8
A8
 E0
E0 E6
E6 N6
N6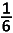 n(n+1)(n+2)
n(n+1)(n+2)
 F0
F0 F2
F2 J0
J0 K2
K2 R4
R4